Calculons l'inverse de 7 pour toutes les bases de forme 3+7n; la longueur de la période est alors 7 - 1 = 6.
Pour une meilleure symbolisation des chiffres dans une base élevée (>10 si n>1) ceux-ci seront, par convention, représentés par leurs expressions en base 10.
(Si l'on veut en effet calculer en base 100000 il serait difficile de créer ou mémoriser ce nombre de symbole :-)
|
|
1° chiffre |
2° chiffre |
3° chiffre |
4° chiffre |
5° chiffre |
6° chiffre |
|
|
n |
base |
||||||
|
0 |
3 |
0 |
1 |
0 |
2 |
1 |
2 |
|
1 |
10 |
1 |
4 |
2 |
8 |
5 |
7 |
|
2 |
17 |
2 |
7 |
4 |
14 |
9 |
12 |
|
3 |
24 |
3 |
10 |
6 |
20 |
13 |
17 |
|
. |
. |
. |
. |
. |
. |
. |
. |
|
n |
3+7n |
n |
1+3n |
2n |
2+6n |
1+4n |
2+5n |
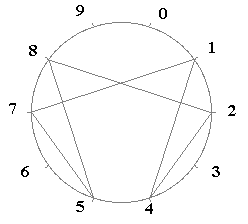
On retrouve alors, à la deuxième ligne lorsque n=1 et que la base est égale à 10, la fameuse période de 1/7 en base 10: 142857.
Considérons maintenant les représentations graphiques:
n = 1
1/7 en base 10 = (3 + 1x7)

On retrouve ici l'ennéagramme cher à Gurdgieff.
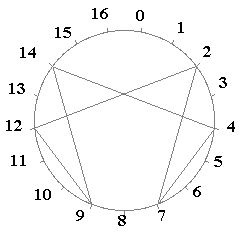
Le graphe reste similaire pour n = 2, la base est alors égale à 17.
n = 2
1/7 en base 17 = (3 + 2x7)
2 - 7 - 4 - 14 - 9 - 12
Faisant croître n vers l'infini, on peut en tirer la représentation formulaire des chiffres de la période, et le graphe général des inverses de:
1/7 en base 3+7n:
n __ 1+3n __ 2n __ 2+6n __ 1+4n __ 2+5n
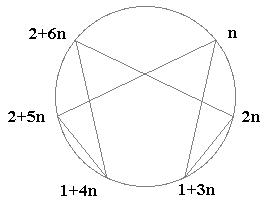
Les points visités s'organisent alors de manière à partager le cercle en 7 parties égales.
La longueur de la période est égale à 6 ((p - 1) avec p premier égal 7).
C'est cette représentation où n tend vers l'infini qui doit être retenue pour le numéroscope,
mais encore la découverte des premiers pour lesquels cette période est unique dans une base donnée.
Cette période unique définit la forme primaire du numéroscope.
Il en existe une forme altérée, ne serait-ce que pour l'observation de la base 4.
Cette forme altérée du numéroscope se doit de calculer toutes les fractions d'un premier p dans les bases où il n'existe pas
de périodes uniques
NB: On constate d'autre part, que si la période (de longueur 6) existe pour n=0 (en base 3), elle ne produit pas assez de points (de chiffres en base 3) pour réaliser ces figures.
n=0 est une exception du numéroscope.